A torzítás mértéke
Az úgynevezett Lie Factor (hivatalos magyar megfelelő fordítás hiányában) annak a mértéke, hogy adott vizualizáció mennyire torzított módon ábrázolja az adatok egymáshoz való viszonyát. Az eredeti megfogalmazás szerint: “The representation of numbers, as physically measured on the surface of the graphic itself, should be directly proportional to the quantities represented.” [Edward Tufte, 1991] mely magyarul valahogy így hangzik: Az értékekhez tartozó ábrázolások méreteinek reprezentálniuk kell azok egymáshoz viszonyított arányát. A Lie Factor maga egy szám, melynek kiszámítása egy egyszerű képlet segítségével történik:
Az így kapott számot a következő táblázat segít értelmezni:
(A gyakorlatban egyébként a minimális torzítás még elfogadott, tehát 0,95 < Lie Factor < 1,05 még torzítatlannak tekinthető.)
Nézzük meg mindezt egy egyszerű példán keresztül is!
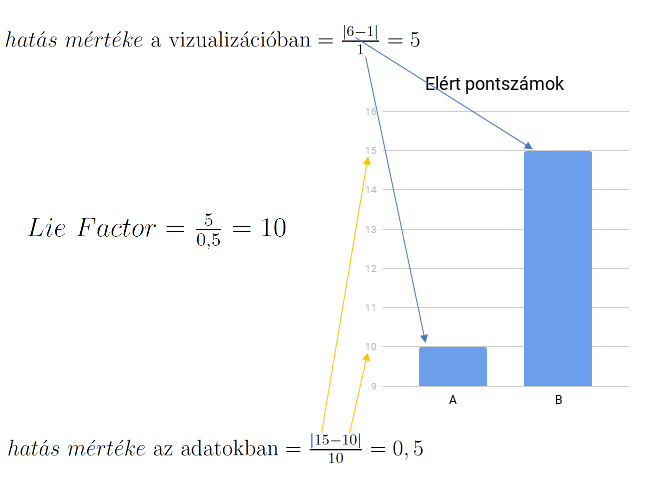Az ábrán jól látható, hogy mivel a függőleges tengely csak 9-től indul, így az arányok jelentősen eltorzulnak a két oszlop között. A 10 pontos oszlopot 1 egységnek tekintve, a 15 pontos oszlop 6 egységnyi területével szemben a torzítás mértéke már így is érzékelhető. Természetesen a 15 mindig nagyobb lesz, mint a 10, de nem mindegy, hogy ez milyen arányban kerül ábrázolásra. Ha a függőleges tengely 0-tól indulna, és egyenletes mértékben ábrázolná mind a két oszlopot, akkor a Lie Factor értéke 1 lenne. Ez nem azt jelenti tehát, hogy a két oszlop mérete megegyezne, hanem azt, hogy az ábrázolt arányuk azonos lenne az adatok arányával.
Apró trükkök, emlékezetes példák
Az eddigiek ismeretében a következő vizualizációkban már sok csalafintaságra felfigyelhetünk, azonban egy-két eddig ismeretlen kisebb trükk is megbújik ezeken a látványos, ugyanakkor becsapós ábrákon. A teljesség igénye nélkül, csak felsorolásszerűen említjük meg ezeket.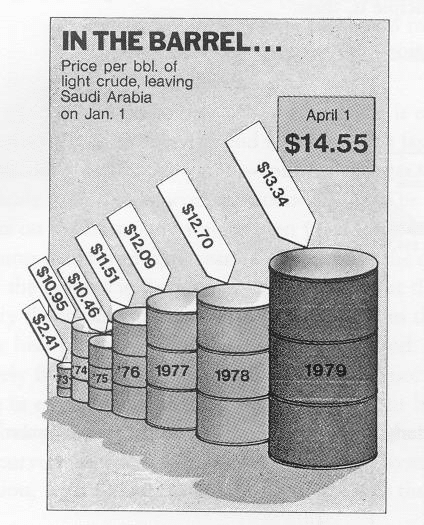
A fenti ábrán 3 dimenziós hordókat láthatunk, melyek egymást kitakarva - s részben a perspektivikus ábrázolás miatt - a háttérben lévő hordókat kisebbnek, a legelöl lévőket pedig még nagyobbnak érzékeltetik. Habár az évszámok léptéke megegyezik, az egyes oszlopok, azaz hordók szélessége is változik, így a nagyobb évszám nem csak függőlegesen, hanem vízszintesen is egyre dominánsabb. További látványos trükk lehetett volna a hordók feletti április 1-jei felirat helyett egy még nagyobb hordó feltüntetése, mely kilóg az ábrából.
A hordók felületét tekintve a Lie Factor = 9,4, viszont a térfogat tekintetében ez az érték már 59,4 (ez rekord közeli eredmény torzításban).
Ezen az utat reprezentáló, perspektivikus ábrázolással készült adatvizualizáción - ami igazából egy eltorzított sávdiagram - még pontosabban mérhető a Lie Factor, ugyanis csak az egyes évekhez és üzemanyag mennyiségekhez tartozó egyenesek hosszát kell összehasonlítani, ahogyan az ábrán látható magyarázó címkék is ezt jelzik. Talán ami első ránézésre még feltűnő lehet, hogy az út “felénk tart”, azaz a jövő a mi irányunkban van, pedig ezt pont fordítva szokás ábrázolni, hogy a jövő van előrefelé az úton, a távolban. Továbbá a jobb oldali gallon értékeket feltüntető tengelyen, a perspektív ábrázolásból adódóan különböző a távolságok mértéke az egyes számértékek között, így például a 18 és 19 sokkal közelebb helyezkedik el egymáshoz, mint a 26 és 27. Sőt az is kicsit megtévesztő lehet, hogy míg a szóban forgó jobb oldali tengelyen a nagyobb értékekhez nagyobb méretű felirat is tartozik, a bal oldali évszámokat feltüntető tengelyen a feliratok mérete nem változik.
Jelen esetben az így kapott Lie Factor = 14,8.
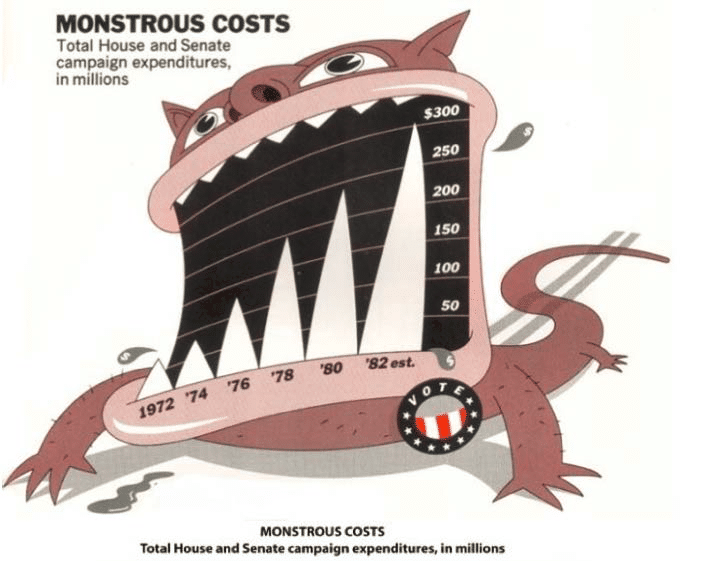Ebben a helyzetben a látványos ábra elvonja a figyelmet a lényegről, az adatokról. A vízszintes tengely görbülése is azt eredményezi, hogy a bal oldali fogak (oszlopok) ugyanakkora értéknél alacsonyabbak, mint a jobb oldaliak. Emiatt a torzítás miatt nem is számítható ki pontosan a Lie Factor, de nagyjából 2,5-re tehető. Arra is érdemes odafigyelni, hogy az 1982-es adat csak becslés (est.)!
Az ábrázolás sajátosságai miatt a fenti ábrán is csak becsülni lehet a Lie Factor-t, mely nagyjából 2,1-re tehető. Megemlítenék azonban két másik trükköt - az egyik a jobb oldali figurához képest történő ábrázolás. Nem véletlen, hogy csak a legnagyobb szikra csík (oszlop) kúszik a figura feje fölé, a többi pedig maximum szemmagasságba ér neki. A másik csel is ehhez kapcsolódik, hiszen a legnagyobb szikra keretből való kilépése még inkább azt érzékelteti, hogy ez az érték jelentősen túllő a többin.
Utóbbi két ábránk kapcsán még további problémakörök is felmerülhetnek, azonban ezeket már nem részleteznénk itt, viszont aki kíváncsi, az nyugodtan nézzen utána a Data-Ink Ratio és a Chartjunk fogalmának is (szintén Edward Tufte-től), melyekre rengeteg “jó” példát lehet találni.
